La demostración de Abel-Ruffini tiene una desventaja: es técnica y dificulta el entender las razones por las que ecuaciones de grado 1, 2, 3 y 4 se resuelven con una fórmula, pero las de grado 5 —y mayores— no se pueden resolver de esta manera. En la actualidad, se usa una teoría basada en las ideas de Evariste Galois —un matemático francés contemporáneo de Abel— para demostrarlo. Sin embargo, antes de llegar a la teoría de Galois, tendremos que preparar unas nociones sobre polinomios.
Los términos de la forma:
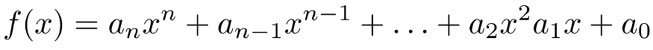 (30)
(30)
se llaman polinomios en la variable con coeficientes a0, a1,. . ., an . Si , an ≠ 0 entonces n es el grado de f(x) .
En lo que sigue, será importante considerar polinomios sobre diferentes campos: si todos los coeficientes pertenecen al campo K de los números racionales, diremos que f (x) es un polinomio racional. Los polinomios racionales forman un conjunto [x] donde es posible sumar y multiplicar también hay elementos neutros aditivos y multiplicativos e inversos aditivos, pero no existen inversos multiplicativos. Se dice que [x] es un anillo. De manera similar si K es un campo, denotamos con K [x]al anillo de polinomios con coeficientes en K. Un caso importante son los números complejos: 
Si en la expresión 30 se sustituye la variable x por un número s, entonces se obtiene un número que se denota por f (s). Un número s que satisface f (s) = 0 se llama raíz del polinomio f (x). De hecho la notación f (x) sugiere que se trata de una función y eso es cierto: se trata de la función polinomial que se obtiene al sustituir diferentes valores para x. Si s es raíz de f (x), entonces f (x) se puede factorizar:
f (x) = g(x) . (x –s),
es decir, existe un polinomio g(x) con grado menor que f(x) y factor lineal de x – s , tal que su producto es f(x). Pero los coeficientes del polinomio g (x) serán expresiones que pueden involucrar a la raíz , como se explica en el siguiente ejemplo.

El teorema fundamental del álgebra tiene una interpretación alterna: cada polinomio 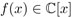 se puede escribir como producto:
se puede escribir como producto:
an· (x – s1)· (x – s2) · …· (x – sn ) (31)
donde s1, …, sn son las soluciones de la ecuación (29). En otras palabras, cada polinomio con coeficientes complejos se descompone en factores lineales. Por ejemplo:
x2 +1= (x – i)(x +i). (32)
dado que ±i son las dos soluciones de la ecuación x2 + 1 = 0. El polinomio 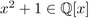 no se descompone en factores lineales pues ±i no son racionales, pero
no se descompone en factores lineales pues ±i no son racionales, pero 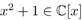 sí se descompone como. La descomposición en (31) es única en el siguiente sentido: el factor an es único y los elementos s1, …, sn son únicos salvo permutación, es decir, dos representaciones (31) —si son iguales— sólo pueden distinguirse en el orden en que se escriben los factores (x – s1 ), ..., (x – sn ).
sí se descompone como. La descomposición en (31) es única en el siguiente sentido: el factor an es único y los elementos s1, …, sn son únicos salvo permutación, es decir, dos representaciones (31) —si son iguales— sólo pueden distinguirse en el orden en que se escriben los factores (x – s1 ), ..., (x – sn ).
Hemos llegado a un punto crucial: ¿cuál es el número i y cuál es –i ? Recordemos que antes simplemente postulamos su existencia y vimos que podíamos hacer cálculos con números de la forma a + bi. El número es una solución de la ecuación x2 +1 =0, mientras que la otra es –i. Pero no hay ninguna manera de saber cuál es cuál, sólo sabemos que una solución es la inversa aditiva de la otra. Si otra persona escoge j = –i como solución, entonces obtiene una copia igual de números complejos. Lo anterior se puede decir todavía de otra manera: hay una simetría en los números complejos, donde la función:
se llama conjugación. La conjugación es un automorfismo, es decir, es biyectiva y conserva las operaciones de adición, multiplicación y la formación de inversos:
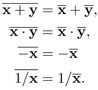
Los números fijos bajo la conjugación son los números reales, dado que 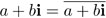 implica que b = 0.
implica que b = 0.
Sin embargo, en la realidad no necesitamos los números reales para estudiar la ecuación x2 + 1 = 0. Los coeficientes son números enteros. El campo más pequeño (respecto a la contención de conjuntos) que contiene a los coeficientes 0,1 es 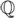 , el campo de los números racionales. Por ejemplo, el campo más pequeño que contiene los coeficientes y las soluciones ±i es el campo K, cuyos elementos son de la forma a+ bi, donde
, el campo de los números racionales. Por ejemplo, el campo más pequeño que contiene los coeficientes y las soluciones ±i es el campo K, cuyos elementos son de la forma a+ bi, donde  Se dice que K es el campo de descomposición del polinomio x2 + 1 sobre
Se dice que K es el campo de descomposición del polinomio x2 + 1 sobre 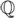 , dado que x2 + 1 se descompone K en factores lineales (32) y es el campo más chico con esta propiedad.
, dado que x2 + 1 se descompone K en factores lineales (32) y es el campo más chico con esta propiedad.
En general, fijamos un polinomio f (x) como en (30), con coeficientes 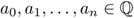 , y definimos K como el campo de descomposición de f (x), es decir, el campo más pequeño que contiene
, y definimos K como el campo de descomposición de f (x), es decir, el campo más pequeño que contiene 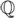 y todas las soluciones de la ecuación f (x) = 0. Por ejemplo, si f(x) = x3 – 2 es el polinomio a descomponer, entonces
y todas las soluciones de la ecuación f (x) = 0. Por ejemplo, si f(x) = x3 – 2 es el polinomio a descomponer, entonces 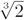 es una raíz y f(x) se descompone como:
es una raíz y f(x) se descompone como:
en K[x], K donde es el campo:
Con ayuda de la fórmula general para resolver ecuaciones cuadráticas y después de algunas transformaciones algebraicas, se obtiene que el segundo factor de (33) se puede escribir como:
donde 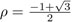 es una tercera raíz primitiva de la unidad, es decir, una solución de la ecuación x3= 1 que no es solución de una ecuación xp = 1para p < 3. Las tres raíces de f(x) = x3 – x -1 son entonces
es una tercera raíz primitiva de la unidad, es decir, una solución de la ecuación x3= 1 que no es solución de una ecuación xp = 1para p < 3. Las tres raíces de f(x) = x3 – x -1 son entonces 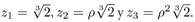
En seguida, denotamos con 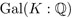 al conjunto de todos los automorfismos de K que fijan los elementos de
al conjunto de todos los automorfismos de K que fijan los elementos de 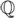 punto por punto, es decir φ (z) = z para cada
punto por punto, es decir φ (z) = z para cada  y cada
y cada 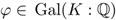 . Por construcción,
. Por construcción, 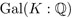 es un grupo, dado que podemos componer dos automorfismos que fijan
es un grupo, dado que podemos componer dos automorfismos que fijan 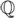 para obtener otra vez un automorfismo que fija
para obtener otra vez un automorfismo que fija 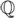 ; la identidad de Ksiempre es un elemento de
; la identidad de Ksiempre es un elemento de 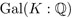 y un inverso de un elemento de
y un inverso de un elemento de 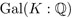 es, nuevamente, un elemento de
es, nuevamente, un elemento de 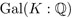 .
.
El grupo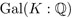 se llama grupo de Galois de K sobre
se llama grupo de Galois de K sobre 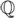 . En general, un grupo es un conjunto con una operación binaria —como una multiplicación, adición, composición o cualquier otra operación binaria— que tiene elemento neutro e inverso.
. En general, un grupo es un conjunto con una operación binaria —como una multiplicación, adición, composición o cualquier otra operación binaria— que tiene elemento neutro e inverso.
Cada elemento φ de 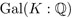 fija los coeficientes del polinomio f (x) , es decir, φ (ai ) = ai, dado que ai ∈
fija los coeficientes del polinomio f (x) , es decir, φ (ai ) = ai, dado que ai ∈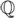 . Por otro lado, el automorfismo φ induce una función entre los polinomios en K[x] :
. Por otro lado, el automorfismo φ induce una función entre los polinomios en K[x] :
Esta función también conserva suma, multiplicación, elementos neutros e inversos aditivos de K [x] , dado que φ es un automorfismo que fija los elementos de K . Esto tiene una fuerte implicación si aplicamos φ a la ecuación:
entonces, el lado izquierdo no cambia. El lado derecho, an · (x – φ ( s1 )) ·…· (x – φ ( sn ))es una factorización de f(x) . Como ésta es única, concluimos que φ induce una permutación de las raíces s1, …, sn .
Por otro lado, si 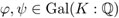 inducen la misma permutación en las raíces s1, …, sn, entonces φ = ψ —esto sigue de que K es el campo más pequeño que contiene
inducen la misma permutación en las raíces s1, …, sn, entonces φ = ψ —esto sigue de que K es el campo más pequeño que contiene 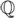 y s1, …, sn, un argumento que aquí no detallamos. Como sólo hay un número finito de permutaciones de s1, …, sn concluimos que
y s1, …, sn, un argumento que aquí no detallamos. Como sólo hay un número finito de permutaciones de s1, …, sn concluimos que 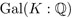 es un grupo finito. Por ejemplo, si f(x) = x2 + 1, entonces
es un grupo finito. Por ejemplo, si f(x) = x2 + 1, entonces 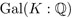 contiene dos elementos: la conjugación y la identidad.
contiene dos elementos: la conjugación y la identidad.
Si f(x) = x4 + 1, entonces los cuatro números:
son raíces de f(x), como se comprueba al sustituir y, dado que f(x) tiene grado 4 , no puede tener más raíces. El campo de descomposición K contiene, por lo tanto, estos cuatro números pero también al cuadrado de z1:
y además, la suma:
Por lo tanto, K contiene números de la forma 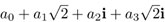 , donde los coeficientes a0, a1 y a3 son números racionales. No es difícil ver que, en efecto, K consiste exactamente en estos números: hay que ver que el conjunto formado por dichos números es cerrado bajo la multiplicación e inversos multiplicativos.
, donde los coeficientes a0, a1 y a3 son números racionales. No es difícil ver que, en efecto, K consiste exactamente en estos números: hay que ver que el conjunto formado por dichos números es cerrado bajo la multiplicación e inversos multiplicativos.
Veamos ahora cómo los elementos del grupo 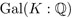 permutan las raíces: si por ejemplo φ (z1) =z3, entonces φ (z3) = φ (–z1) = φ (–1) φ (z1) = –z3 = z1, ya que φ(–1) = –1. Además,
permutan las raíces: si por ejemplo φ (z1) =z3, entonces φ (z3) = φ (–z1) = φ (–1) φ (z1) = –z3 = z1, ya que φ(–1) = –1. Además, 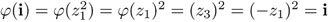 . Entonces,
. Entonces, 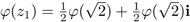 , que debe ser igual a
, que debe ser igual a 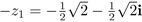 . Lo anterior muestra que
. Lo anterior muestra que  . Con ello se concluye que φ(z3) = –z3 = z4 y, por lo tanto, φ intercambia z1 con z3 y z2 con z4 . De manera similar se puede mostrar que el automorfismo ψ que satisface ψ(z1) = z2 intercambia z1con z2 y z3 con z4, y que el automorfismo η que satisface η( z1 ) = z4 intercambia z1 con z4 y z2 con z3. Con la identidad —que es el automorfismo que deja todo fijo— se obtiene un grupo de 4 automorfismos.
. Con ello se concluye que φ(z3) = –z3 = z4 y, por lo tanto, φ intercambia z1 con z3 y z2 con z4 . De manera similar se puede mostrar que el automorfismo ψ que satisface ψ(z1) = z2 intercambia z1con z2 y z3 con z4, y que el automorfismo η que satisface η( z1 ) = z4 intercambia z1 con z4 y z2 con z3. Con la identidad —que es el automorfismo que deja todo fijo— se obtiene un grupo de 4 automorfismos.
Se observa que 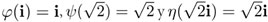 . El conjunto de todos los números y que satisfacen φ (y)= y, forma un campo L que contiene
. El conjunto de todos los números y que satisfacen φ (y)= y, forma un campo L que contiene 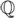 y que es contenido en K . Se llama el campo de puntos fijos de φ. Más general, a los campos que contienen
y que es contenido en K . Se llama el campo de puntos fijos de φ. Más general, a los campos que contienen 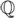 y que están contenidos en K se les llama campos intermedios y juegan un papel importante en el resto de esta sección. El campo de puntos fijos de φ es justamente el campo
y que están contenidos en K se les llama campos intermedios y juegan un papel importante en el resto de esta sección. El campo de puntos fijos de φ es justamente el campo 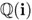 , que se llama el campo de los números de Gauss, en honor a Carl Friedrich Gauss. El campo de los puntos fijos de ψ es
, que se llama el campo de los números de Gauss, en honor a Carl Friedrich Gauss. El campo de los puntos fijos de ψ es 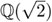 y el de η es
y el de η es 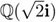 .
.